邵雍的方圆六十四卦
九数
宋代易学别具一格,以河图洛书的传世为先声,到邵雍创立先天象数学为顶峰。这一时期的学问,往往归结为一张图。河图如此,洛书如此,太极图如此,邵雍的学说也如此。
邵雍的学说,归结为一张《伏羲先天六十四卦次序方圆图》。这个名字看上去似乎很长,仔细推敲,每个字都有意思。伏羲是学说的本源;先天表明区别于后天;六十四卦规模较大,体系更深遂;次序言其立意;方圆以象天地;图示其形式。
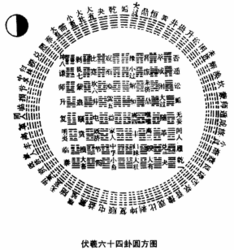
这个图,看上去是无字天书。图上只有卦,卦中只有阴阳爻。全图无一字,怎么理解呢?
邵雍创立此图,推演了元会运世的庞大时间计算体系。《皇极经世》是元会运世这一学说的运用。在前面的短文中,我们见过一点,《观物外篇》中记载了邵雍曾经推演过“无极之数”,我们已经知道所用计数单位是非常庞大的数字,写出来有八十一位数字之多。基本上,这个推演,立足于圆图。
那么方图有何妙处呢?看上去,方图不过是圆图的分宫排列。将六十四卦分为八宫,每宫八卦。大体上,一般人就是这样理解的方图。如果仔细看的话,可以发现排列具有相似的特性,八宫的次序,与每宫内八卦的次序,完全一致,都是先天八卦次序的体现。也可以说,这个排列具有全息的特性。
在这篇短文中,九数要指出,无论采用何种形式的卦数对映,这个方图本身都是一个八行八列的数字方阵,非常奇妙的是,这个数阵遵循我们在前面的短文所揭示的洛书旋机方程组。
洛书旋机方程组
a+b+c+d=e+f+g+h
a^2+b^2+c^2+d^2=e^2+f^2+g^2+h^2
a^3+b^3+c^3+d^3=e^3+f^3+g^3+h^3
○○○○○○○○
○●●●●●●○
○●○○○○●○
○●○●●○●○
○●○●●○●○
○●○○○○●○
○●●●●●●○
○○○○○○○○
我们将看到,原来在洛书中发现的转盘结构,同样成立。很明显,八行八列的方阵,可以分解出四层转盘。
(一)八卦序数的形式
如果将卦换成在先天八卦中的序数,那么方图可以有个简单点的书写形式。
卦序:一,二,三,四,五,六,七,八
卦名:乾,兑,离,震,巽,坎,艮,坤
八八,八七,八六,八五,八四,八三,八二,八一
七八,七七,七六,七五,七四,七三,七二,七一
六八,六七,六六,六五,六四,六三,六二,六一
五八,五七,五六,五五,五四,五三,五二,五一
四八,四七,四六,四五,四四,四三,四二,四一
三八,三七,三六,三五,三四,三三,三二,三一
二八,二七,二六,二五,二四,二三,二二,二一
一八,一七,一六,一五,一四,一三,一二,一一
这个用卦序数字书写的形式,为古人所创。记录的格式为:下卦序数在前,上卦序数在后。
下面这个例子,我们取数的时候,在最外层转盘,每次取四分之一圆周。
正向取数
88→87→86→85→84→83→82,81→71→61→51→41→31→21,
11→12→13→14→15→16→17,18→28→38→48→58→68→78;
反向取数
88→78→68→58→48→38→28,18→17→16→15→14→13→12,
11→21→31→41→51→61→71,81→82→83→84→85→86→87。
数字等和
88878685848382+81716151413121+11121314151617+18283848586878
=199 999 999 999 998
88786858483828+18171615141312+11213141516171+81828384858687
=199 999 999 999 998
平方等和
88878685848382^2+81716151413121^2+11121314151617^2+18283848586878^2
=15 034 932 947 514 333 190 280 480 138
88786858483828^2+18171615141312^2+11213141516171^2+81828384858687^2
=15 034 932 947 514 333 190 280 480 138
立方等和
88878685848382^3+81716151413121^3+11121314151617^3+18283848586878^3
=1 255 239 942 127 157 426 142 650 748 900 214 579 279 794
88786858483828^3+18171615141312^3+11213141516171^3+81828384858687^3
=1 255 239 942 127 157 426 142 650 748 900 214 579 279 794
(二)0-1爻数的形式
莱布尼兹是一位德国人,生活在我们之前大约三百年。他发明了二進制,只用数字0和1表示数。当年他与在清朝的传教士来往,世上至今仍然留有那时他们的书信。历史记载,莱布尼兹在德国见过邵雍的方圆图,他曾经用放大镜仔细观察八卦,发现八卦是由阳爻(―)和阴爻(- -)两种符号组成。
莱布尼兹的天才在于,他以数解卦。这个方法开辟了沟通算术与易学的道路。按照他的观点,所谓阴阳可以数字化,阳爻用数字1表示,阴爻用数字0表示。这样每个卦都成了由0和1构成的六位数。特别的,他认为采用二進制来计算,是最简单的。
卦数:111,110,101,100,011,010,001,000
卦名:乾,兑,离,震,巽,坎,艮,坤
六十四卦方图
000000,000001,000010,000011,000100,000101,000110,000111
001000,001001,001010,001011,001100,001101,001110,001111
010000,010001,010010,010011,010100,010101,010110,010111
011000,011001,011010,011011,011100,011101,011110,011111
100000,100001,100010,100011,100100,100101,100110,100111
101000,101001,101010,101011,101100,101101,101110,101111
110000,110001,110010,110011,110100,110101,110110,110111
111000,111001,111010,111011,111100,111101,111110,111111
下面这个例子,每个数取的是四个卦。少取点数似乎好些,由0和1组成的数容易让人看花眼睛。(需要注意的是,这里本来是取的二進制数,计算的时候,是当作十進制数的。原因很简单,我的计算器是算十進制数的,哈哈哈。)
正向取数
000000→000001→000010→000011,
000111→001111→010111→011111,
111111→111110→111101→111100,
111000→110000→101000→100000;
反向取数
000000→001000→010000→011000,
111000→111001→111010→111011,
111111→110111→101111→100111,
000111→000110→000101→000100。
数字等和
000000000001000010000011+000111001111010111011111+
111111111110111101111100+111000110000101000100000
=222 222 222 222 222 222 222 222
000000001000010000011000+111000111001111010111011+
111111110111101111100111+000111000110000101000100
=222 222 222 222 222 222 222 222
平方等和
000000000001000010000011^2+000111001111010111011111^2+
111111111110111101111100^2+111000110000101000100000^2
=24 666 715 753 404 622 091 308 731 084 040 397 351 528 664 442
000000001000010000011000^2+111000111001111010111011^2+
111111110111101111100111^2+000111000110000101000100^2
=24 666 715 753 404 622 091 308 731 084 040 397 351 528 664 442
立方等和
000000000001000010000011^3+000111001111010111011111^3+
111111111110111101111100^3+111000110000101000100000^3
=2 739 377 179 751 250 458 290 824 183 408 702 660 561 246 413 839 743 880 784 254 854 961 962
000000001000010000011000^3+111000111001111010111011^3+
111111110111101111100111^3+000111000110000101000100^3
=2 739 377 179 751 250 458 290 824 183 408 702 660 561 246 413 839 743 880 784 254 854 961 962
(三)六十四卦序数的形式
乾坤立极,基本上六十四卦序数,可以看作是圆图按照太极图中的S形路线运行,始于乾卦,终于坤卦。
64,63,62,61,60,59,58,57
56,55,54,53,52,51,50,49
48,47,46,45,44,43,42,41
40,39,38,37,36,35,34,33
32,31,30,29,28,27,26,25
24,23,22,21,20,19,18,17
16,15,14,13,12,11,10,09
08,07,06,05,04,03,02,01
从算术的角度看,(二)和(三)可以连系的,比如乾卦111111,化二進制为十進制,得到63,序数为64-63=1;坤卦为000000,化二進制为十進制,得到0,序数为64-0=64。总之,所化出的数与序数之和为64。
这种序数形式,看上去最简单,我们作个透彻的计算。对于各层转盘,我们都选取完整的周天形式。这样看上去,数字有点大,但更容易理解。
第四层转盘
64,63,62,61,60,59,58,57
56,●,●,●,●,●,●,49
48,●,○,○,○,○,●,41
40,●,○,●,●,○,●,33
32,●,○,●,●,○,●,25
24,●,○,○,○,○,●,17
16,●,●,●,●,●,●,09
08,07,06,05,04,03,02,01
正向取数
64→63→62→61→60→59→58→57→49→41→33→25→17→09→01→02→03→04→05→06→07→08→16→24→32→40→48→56,
57→49→41→33→25→17→09→01→02→03→04→05→06→07→08→16→24→32→40→48→56→64→63→62→61→60→59→58,
01→02→03→04→05→06→07→08→16→24→32→40→48→56→64→63→62→61→60→59→58→57→49→41→33→25→17→09,
08→16→24→32→40→48→56→64→63→62→61→60→59→58→57→49→41→33→25→17→09→01→02→03→04→05→06→07;
反向取数
64→56→48→40→32→24→16→08→07→06→05→04→03→02→01→09→17→25→33→41→49→57→58→59→60→61→62→63,
08→07→06→05→04→03→02→01→09→17→25→33→41→49→57→58→59→60→61→62→63→64→56→48→40→32→24→16,
01→09→17→25→33→41→49→57→58→59→60→61→62→63→64→56→48→40→32→24→16→08→07→06→05→04→03→02,
57→58→59→60→61→62→63→64→56→48→40→32→24→16→08→07→06→05→04→03→02→01→09→17→25→33→41→49。
数字等和
64636261605958574941332517090102030405060708162432404856+
57494133251709010203040506070816243240485664636261605958+
01020304050607081624324048566463626160595857494133251709+
08162432404856646362616059585749413325170901020304050607
=131 313 131 313 131 313 131 313 131 313 131 313 131 313 131 313 131 313 130
64564840322416080706050403020109172533414957585960616263+
08070605040302010917253341495758596061626364564840322416+
01091725334149575859606162636456484032241608070605040302+
57585960616263645648403224160807060504030201091725334149
=131 313 131 313 131 313 131 313 131 313 131 313 131 313 131 313 131 313 130
平方等和
64636261605958574941332517090102030405060708162432404856^2+
57494133251709010203040506070816243240485664636261605958^2+
01020304050607081624324048566463626160595857494133251709^2+
08162432404856646362616059585749413325170901020304050607^2
=7 551 087 995 878 725 334 014 243 927 581 795 597 922 585 583 117 298 186 419 438 614 990 707 696 154 807 055 673 676 993 515 723 639 118 321 967 630
64564840322416080706050403020109172533414957585960616263^2+
08070605040302010917253341495758596061626364564840322416^2+
01091725334149575859606162636456484032241608070605040302^2+
57585960616263645648403224160807060504030201091725334149^2
=7 551 087 995 878 725 334 014 243 927 581 795 597 922 585 583 117 298 186 419 438 614 990 707 696 154 807 055 673 676 993 515 723 639 118 321 967 630
立方等和
64636261605958574941332517090102030405060708162432404856^3+
57494133251709010203040506070816243240485664636261605958^3+
01020304050607081624324048566463626160595857494133251709^3+
08162432404856646362616059585749413325170901020304050607^3
=460 636 444 141 622 348 613 229 165 606 410 489 847 544 723 509 241 208 504 510 360 597 832 791 268 731 233 441 264 301 171 317 649 555 934 959 525 312 873 153 647 913 892 855 405 153 067 119 979 706 109 436 130 130 324 300
64564840322416080706050403020109172533414957585960616263^3+
08070605040302010917253341495758596061626364564840322416^3+
01091725334149575859606162636456484032241608070605040302^3+
57585960616263645648403224160807060504030201091725334149^3
=460 636 444 141 622 348 613 229 165 606 410 489 847 544 723 509 241 208 504 510 360 597 832 791 268 731 233 441 264 301 171 317 649 555 934 959 525 312 873 153 647 913 892 855 405 153 067 119 979 706 109 436 130 130 324 300
第三层转盘
55,54,53,52,51,50
47,○,○,○,○,42
39,○,●,●,○,34
31,○,●,●,○,26
23,○,○,○,○,18
15,14,13,12,11,10
正向取数
55→54→53→52→51→50→42→34→26→18→10→11→12→13→14→15→23→31→39→47,
50→42→34→26→18→10→11→12→13→14→15→23→31→39→47→55→54→53→52→51,
10→11→12→13→14→15→23→31→39→47→55→54→53→52→51→50→42→34→26→18,
15→23→31→39→47→55→54→53→52→51→50→42→34→26→18→10→11→12→13→14;
反向取数
55→47→39→31→23→15→14→13→12→11→10→18→26→34→42→50→51→52→53→54,
15→14→13→12→11→10→18→26→34→42→50→51→52→53→54→55→47→39→31→23,
10→18→26→34→42→50→51→52→53→54→55→47→39→31→23→15→14→13→12→11,
50→51→52→53→54→55→47→39→31→23→15→14→13→12→11→10→18→26→34→42。
数字等和
5554535251504234261810111213141523313947+
5042342618101112131415233139475554535251+
1011121314152331394755545352515042342618+
1523313947555453525150423426181011121314
=13 131 313 131 313 131 313 131 313 131 313 131 313 130
5547393123151413121110182634425051525354+
1514131211101826344250515253545547393123+
1018263442505152535455473931231514131211+
5051525354554739312315141312111018263442
=13 131 313 131 313 131 313 131 313 131 313 131 313 130
平方等和
5554535251504234261810111213141523313947^2+
5042342618101112131415233139475554535251^2+
1011121314152331394755545352515042342618^2+
1523313947555453525150423426181011121314^2
=59 620 932 633 272 101 557 033 624 364 107 030 030 229 391 442 090 208 143 379 650 172 917 124 650 532 330
5547393123151413121110182634425051525354^2+
1514131211101826344250515253545547393123^2+
1018263442505152535455473931231514131211^2+
5051525354554739312315141312111018263442^2
=59 620 932 633 272 101 557 033 624 364 107 030 030 229 391 442 090 208 143 379 650 172 917 124 650 532 330
立方等和
5554535251504234261810111213141523313947^3+
5042342618101112131415233139475554535251^3+
1011121314152331394755545352515042342618^3+
1523313947555453525150423426181011121314^3
=304 144 538 663 064 035 597 763 564 203 196 825 198 363 311 486 104 750 727 213 678 590 087 633 260 202 640 425 385 800 874 084 902 452 485 147 184 503 707 550
5547393123151413121110182634425051525354^3+
1514131211101826344250515253545547393123^3+
1018263442505152535455473931231514131211^3+
5051525354554739312315141312111018263442^3
=304 144 538 663 064 035 597 763 564 203 196 825 198 363 311 486 104 750 727 213 678 590 087 633 260 202 640 425 385 800 874 084 902 452 485 147 184 503 707 550
第二层转盘
46,45,44,43
38,●,●,35
30,●,●,27
22,21,20,19
正向取数
46→45→44→43→35→27→19→20→21→22→30→38,
43→35→27→19→20→21→22→30→38→46→45→44,
19→20→21→22→30→38→46→45→44→43→35→27,
22→30→38→46→45→44→43→35→27→19→20→21;
反向取数
46→38→30→22→21→20→19→27→35→43→44→45,
22→21→20→19→27→35→43→44→45→46→38→30,
19→27→35→43→44→45→46→38→30→22→21→20,
43→44→45→46→38→30→22→21→20→19→27→35。
数字等和
464544433527192021223038+433527192021223038464544+
192021223038464544433527+223038464544433527192021
=1 313 131 313 131 313 131 313 130
463830222120192735434445+222120192735434445463830+
192735434445463830222120+434445463830222120192735
=1 313 131 313 131 313 131 313 130
平方等和
464544433527192021223038^2+433527192021223038464544^2+
192021223038464544433527^2+223038464544433527192021^2
=490 365 663 706 432 397 319 661 630 846 457 505 688 814 801 550
463830222120192735434445^2+222120192735434445463830^2+
192735434445463830222120^2+434445463830222120192735^2
=490 365 663 706 432 397 319 661 630 846 457 505 688 814 801 550
立方等和
464544433527192021223038^3+433527192021223038464544^3+
192021223038464544433527^3+223038464544433527192021^3
=199 904 567 894 749 487 320 584 387 457 469 658 924 655 600 642 685 365 235 173 598 584 351 500
463830222120192735434445^3+222120192735434445463830^3+
192735434445463830222120^3+434445463830222120192735^3
=199 904 567 894 749 487 320 584 387 457 469 658 924 655 600 642 685 365 235 173 598 584 351 500
第一层转盘
37,36
29,28
正向取数
37→36→28→29,36→28→29→37,28→29→37→36,29→37→36→28;
反向取数
37→29→28→36,29→28→36→37,28→36→37→29,36→37→29→28。
数字等和
37362829+36282937+28293736+29373628=131 313 130
37292836+29283637+28363729+36372928=131 313 130
平方等和
37362829^2+36282937^2+28293736^2+29373628^2=4 375 778 026 949 290
37292836^2+29283637^2+28363729^2+36372928^2=4 375 778 026 949 290
立方等和
37362829^3+36282937^3+28293736^3+29373628^3=147 916 527 140 638 905 721 150
37292836^3+29283637^3+28363729^3+36372928^3=147 916 527 140 638 905 721 150
悠然心会,妙处难与君说,这篇短文打开了一扇门,更多的妙算也许会在未来揭示吧。
https://www.zhengjian.org/node/57837